K-Means Cluster Analysis

Dataset
I am using Gapminder dataset for the purpose of running Random Forest experiment

Data Management

In cluster analysis variables with large values contribute more to the distance calculations. Variables measured on different scales should be standardized so that the solution is based on variables measured on larger scales. We standardize the cluster variables to have a mean of 0 and SD of 1. The cluster variables are - income per person, internet use rate, female employment rate, armed force rate, employment rate, life expectancy, urban rate, suicide rate.

Cluster Analysis

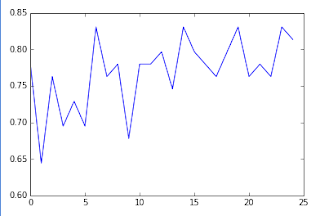
Initially we do not know how many cluster are there in the given dataset. To begin our analysis we calculate the average distance of the observations from the cluster centroids. Then we plot this average distance measure to help us figure out how many clusters may be optimal. This plot is the elbow curve shown above. The average distance decreases as the number of cluster increases. Since the goal of cluster analysis is to minimize the distance between observations and their assigned clusters we want to choose the fewest numbers of clusters that provides a low average distance. The bend in the elbow shows where the average distance value might be leveling off such that adding more clusters doesn't decrease the average distance as much. Closely examining the plot above we see that there are bends at 2 and 3 clusters. To help us figure out which of the solutions is best we will further examine the cluster solutions for at least two and three cluster solutions to see -

• whether they do not overlap
• whether the patterns of means on the clustering variables are unique and meaningful
• whether there are significant differences between the clusters on our external validation variable Polity Score

Canonical Discriminant Analysis

We will plot the clusters in a scatter plot to see whether or not they overlap with each other in terms of their locations in the p dimensional space. However with 8 clustering variables, we will have 8 dimensions. This would be impossible to visualize in a scatter plot. So we use the canonical discriminate analysis. This is data reduction technique that uses smaller number of variables that we linear combination of 8 cluster variables.

Usually, the majority of the variance in the clustering variables will be accounted for by the first

couple of canonical variables and those are the variables that we can plot. The cluster shows good separation, the observations are spread out indicating less correlation among the observations and higher within cluster variance. 

Pattern of Means

Next we can take a look at the pattern of means on the clustering variables for each cluster to see whether they are distinct and meaningful.

From the above means analysis, we see that the third cluster has highest mean income per person, highest mean internet use rate and highest mean urban population. This is keeping with findings from my previous research assignments.

ANOVA - How the clusters differ on Polity Score

We'll use analysis of variance to test whether there are significant differences between clusters on the quantitative POLITYSCORE variable.

The R square and F statistic value from above show that the clusters differ significantly on PolityScore.

Code

# -*- coding: utf-8 -*-
"""
Created on Sun Feb 28 17:10:22 2016

@author: Abhishek
"""

from pandas import Series, DataFrame
import pandas as pd
import numpy as np
import matplotlib.pylab as plt
from sklearn.cross_validation import train_test_split
from sklearn import preprocessing
from sklearn.cluster import KMeans

"""
Data Management
"""
data = pd.read_csv("gapminder.csv")


data['polityscore'] = pd.to_numeric(data['polityscore'], errors='coerce')
data['incomeperperson'] = pd.to_numeric(data['incomeperperson'], errors='coerce')
data['employrate'] = pd.to_numeric(data['employrate'], errors='coerce')
data['femaleemployrate'] = pd.to_numeric(data['femaleemployrate'], errors='coerce')
data['lifeexpectancy'] = pd.to_numeric(data['lifeexpectancy'], errors='coerce')
data['armedforcesrate'] = pd.to_numeric(data['armedforcesrate'], errors='coerce')
data['internetuserate'] = pd.to_numeric(data['internetuserate'], errors='coerce')
data['urbanrate'] = pd.to_numeric(data['urbanrate'], errors='coerce')
data['suicideper100th'] = pd.to_numeric(data['suicideper100th'], errors='coerce')


#upper-case all DataFrame column names
data.columns = map(str.upper, data.columns)

# Data Management
data_clean = data.dropna()

# subset clustering variables
cluster = data_clean[[
'INCOMEPERPERSON',
'INTERNETUSERATE',
'FEMALEEMPLOYRATE',
'ARMEDFORCESRATE',
'EMPLOYRATE',
'LIFEEXPECTANCY',
'URBANRATE',
'SUICIDEPER100TH'
]]
cluster.describe()

# standardize clustering variables to have mean=0 and sd=1
clustervar=cluster.copy()

clustervar['INCOMEPERPERSON']=preprocessing.scale(clustervar['INCOMEPERPERSON'].astype('float64'))
clustervar['INTERNETUSERATE']=preprocessing.scale(clustervar['INTERNETUSERATE'].astype('float64'))
clustervar['FEMALEEMPLOYRATE']=preprocessing.scale(clustervar['FEMALEEMPLOYRATE'].astype('float64'))
clustervar['ARMEDFORCESRATE']=preprocessing.scale(clustervar['ARMEDFORCESRATE'].astype('float64'))
clustervar['EMPLOYRATE']=preprocessing.scale(clustervar['EMPLOYRATE'].astype('float64'))
clustervar['LIFEEXPECTANCY']=preprocessing.scale(clustervar['LIFEEXPECTANCY'].astype('float64'))
clustervar['URBANRATE']=preprocessing.scale(clustervar['URBANRATE'].astype('float64'))
clustervar['SUICIDEPER100TH']=preprocessing.scale(clustervar['SUICIDEPER100TH'].astype('float64'))

# split data into train and test sets
clus_train, clus_test = train_test_split(clustervar, test_size=.3, random_state=123)

# k-means cluster analysis for 1-9 clusters                                                           
from scipy.spatial.distance import cdist
clusters=range(1,10)
meandist=[]

for k in clusters:
    model=KMeans(n_clusters=k)
    model.fit(clus_train)
    clusassign=model.predict(clus_train)
    meandist.append(sum(np.min(cdist(clus_train, model.cluster_centers_, 'euclidean'), axis=1)) 
    / clus_train.shape[0])

"""
Plot average distance from observations from the cluster centroid
to use the Elbow Method to identify number of clusters to choose
"""

plt.plot(clusters, meandist)
plt.xlabel('Number of clusters')
plt.ylabel('Average distance')
plt.title('Selecting k with the Elbow Method')

# Interpret 3 cluster solution
model3=KMeans(n_clusters=3)
model3.fit(clus_train)
clusassign=model3.predict(clus_train)
# plot clusters

from sklearn.decomposition import PCA
pca_2 = PCA(2)
plot_columns = pca_2.fit_transform(clus_train)
plt.scatter(x=plot_columns[:,0], y=plot_columns[:,1], c=model3.labels_,)
plt.xlabel('Canonical variable 1')
plt.ylabel('Canonical variable 2')
plt.title('Scatterplot of Canonical Variables for 3 Clusters')
plt.show()

"""
BEGIN multiple steps to merge cluster assignment with clustering variables to examine
cluster variable means by cluster
"""
# create a unique identifier variable from the index for the 
# cluster training data to merge with the cluster assignment variable
clus_train.reset_index(level=0, inplace=True)
# create a list that has the new index variable
cluslist=list(clus_train['index'])
# create a list of cluster assignments
labels=list(model3.labels_)
# combine index variable list with cluster assignment list into a dictionary
newlist=dict(zip(cluslist, labels))

# convert newlist dictionary to a dataframe
newclus=DataFrame.from_dict(newlist, orient='index')
newclus
# rename the cluster assignment column
newclus.columns = ['cluster']

# now do the same for the cluster assignment variable
# create a unique identifier variable from the index for the 
# cluster assignment dataframe 
# to merge with cluster training data
newclus.reset_index(level=0, inplace=True)
# merge the cluster assignment dataframe with the cluster training variable dataframe
# by the index variable
merged_train=pd.merge(clus_train, newclus, on='index')
merged_train.head(n=100)
# cluster frequencies
merged_train.cluster.value_counts()

"""
END multiple steps to merge cluster assignment with clustering variables to examine
cluster variable means by cluster
"""

# FINALLY calculate clustering variable means by cluster
clustergrp = merged_train.groupby('cluster').mean()
print ("Clustering variable means by cluster")
print(clustergrp)

# validate clusters in training data by examining cluster differences in polityscore using ANOVA
# first have to merge polityscore with clustering variables and cluster assignment data 
polityscore_data=data_clean['POLITYSCORE']

# split polityscore data into train and test sets
polityscore_train, polityscore_test = train_test_split(polityscore_data, test_size=.3, random_state=123)
polityscore_train1=pd.DataFrame(polityscore_train)
polityscore_train1.reset_index(level=0, inplace=True)
merged_train_all=pd.merge(polityscore_train1, merged_train, on='index')
sub1 = merged_train_all[['POLITYSCORE', 'cluster']].dropna()

import statsmodels.formula.api as smf
import statsmodels.stats.multicomp as multi 

gpamod = smf.ols(formula='POLITYSCORE ~ C(cluster)', data=sub1).fit()
print (gpamod.summary())

print ('means for POLITYSCORE by cluster')
m1= sub1.groupby('cluster').mean()
print (m1)

print ('standard deviations for POLITYSCORE by cluster')
m2= sub1.groupby('cluster').std()
print (m2)

mc1 = multi.MultiComparison(sub1['POLITYSCORE'], sub1['cluster'])
res1 = mc1.tukeyhsd()
print(res1.summary())

Lasso Regression

Data Set
I am using Gapminder dataset for the purpose of running Random Forest experiment

Data Management
Similar to previous assignment, I am using binary categorical response variable, ‘polityscore’ and a number of quantitative explanatory variables. The variable polity score ranges from -10 to 10. -10 to -5 is considered Autocratic. -5 to 5 is considered Anocratic. Countries falling in this range is usually politically neutral. 5 to 10 is Democratic. The variable is re-coded such that if a country is Autocratic or Democratic, then the value is 1. Otherwise the value is 0. In LR penalty term is not fair if predictor variables are not on the same scale. That means all the predictors get the same penalty. To remedy this, I will standardize all predictors to have mean = 0 and SD = 1.

Lasso Regression

Variable names and regression coefficients

From the list above we can determine which predictors have shrunk to 0 after applying penalty and subsequently removed from the model. We see that URBANRATE has shrunk to 0. FEMALEEMPLOYRATE and INTERNETUSERATE have strong positive correlation with with target variable and EMPLOYRATE and ARMEDFORCERATE have strong negative correlation with target variable.

This plot shows the relative importance of the predictors at any step of the selection process and they were entered in the model.Comparing against the variable name and regression coefficient list, we see that ARMEDFORCERATE and then LIFEEXPECTANCY enter the model in the beginning. Further down the road, EMPLOYRATE and FEMALEEMPLOYRATE is entered in the model. I assume the reason why armedforcerate and lifeexpectancy predictors were entered first even though they do not have the largest regression coefficient is because initially they had a sharp coefficient slope.

The above plot shows the change in the Mean Square Error vs change in the penalty parameter alpha at each step in the selection process. The average mean square error across all cross validation fold is plotted as the thick black line.

As expected the selected model was less accurate than the test data. Test mean square error was close to training mean square error. This suggests that prediction accuracy was stable across the 2 data sets. The R square values were 0.31 and 0.44, indicating that the training and test data set explained 33 and 44 percent of variance in the polity score bias of a country in the training and test sets respectively.

Code

# -*- coding: utf-8 -*-
"""
Created on Sun Feb 21 11:52:01 2016

@author: Abhishek
"""

#from pandas import Series, DataFrame
import pandas as pd
import numpy as np
import matplotlib.pylab as plt
from sklearn.cross_validation import train_test_split
from sklearn.linear_model import LassoLarsCV
 
#Load the dataset
data = pd.read_csv('gapminder.csv')


# Target Variable
data['polityscore'] = pd.to_numeric(data['polityscore'], errors='coerce')

# Predictor Variables
data['incomeperperson'] = pd.to_numeric(data['incomeperperson'], errors='coerce')
data['employrate'] = pd.to_numeric(data['employrate'], errors='coerce')
data['femaleemployrate'] = pd.to_numeric(data['femaleemployrate'], errors='coerce')
data['lifeexpectancy'] = pd.to_numeric(data['lifeexpectancy'], errors='coerce')
data['armedforcesrate'] = pd.to_numeric(data['armedforcesrate'], errors='coerce')
data['internetuserate'] = pd.to_numeric(data['internetuserate'], errors='coerce')
data['urbanrate'] = pd.to_numeric(data['urbanrate'], errors='coerce')
data['suicideper100th'] = pd.to_numeric(data['suicideper100th'], errors='coerce')

#upper-case all DataFrame column names
data.columns = map(str.upper, data.columns)

# Data Management
data_clean = data.dropna()

# Function that converts Polity score to a binary variable.
def RecodePolityScore (row):
   if row['polityscore']<=-5 or row['polityscore']>=5 :
      return 1
   elif row['polityscore']>-5 and row['polityscore']<5 :
      return 0

#select predictor variables and target variable as separate data sets  
predvar = data_clean[[
'INCOMEPERPERSON',
'INTERNETUSERATE',
'FEMALEEMPLOYRATE',
'ARMEDFORCESRATE',
'EMPLOYRATE',
'LIFEEXPECTANCY',
'URBANRATE',
'SUICIDEPER100TH'
]]

target = data_clean.POLITYSCORE
 
# standardize predictors to have mean=0 and sd=1
predictors=predvar.copy()
from sklearn import preprocessing
predictors['INCOMEPERPERSON']=preprocessing.scale(predictors['INCOMEPERPERSON'].astype('float64'))
predictors['INTERNETUSERATE']=preprocessing.scale(predictors['INTERNETUSERATE'].astype('float64'))
predictors['FEMALEEMPLOYRATE']=preprocessing.scale(predictors['FEMALEEMPLOYRATE'].astype('float64'))
predictors['ARMEDFORCESRATE']=preprocessing.scale(predictors['ARMEDFORCESRATE'].astype('float64'))
predictors['EMPLOYRATE']=preprocessing.scale(predictors['EMPLOYRATE'].astype('float64'))
predictors['LIFEEXPECTANCY']=preprocessing.scale(predictors['LIFEEXPECTANCY'].astype('float64'))
predictors['URBANRATE']=preprocessing.scale(predictors['URBANRATE'].astype('float64'))
predictors['SUICIDEPER100TH']=preprocessing.scale(predictors['SUICIDEPER100TH'].astype('float64'))

# split data into train and test sets
pred_train, pred_test, tar_train, tar_test = train_test_split(predictors, target, 
                                                              test_size=.3, random_state=123)
# specify the lasso regression model
model=LassoLarsCV(cv=10, precompute=False).fit(pred_train,tar_train)

# print variable names and regression coefficients
print(dict(zip(predictors.columns, model.coef_)))

# plot coefficient progression
m_log_alphas = -np.log10(model.alphas_)
ax = plt.gca()
plt.plot(m_log_alphas, model.coef_path_.T)
plt.axvline(-np.log10(model.alpha_), linestyle='--', color='k',
            label='alpha CV')
plt.ylabel('Regression Coefficients')
plt.xlabel('-log(alpha)')
plt.title('Regression Coefficients Progression for Lasso Paths')


# plot mean square error for each fold
m_log_alphascv = -np.log10(model.cv_alphas_)
plt.figure()
plt.plot(m_log_alphascv, model.cv_mse_path_, ':')
plt.plot(m_log_alphascv, model.cv_mse_path_.mean(axis=-1), 'k',
         label='Average across the folds', linewidth=2)
plt.axvline(-np.log10(model.alpha_), linestyle='--', color='k',
            label='alpha CV')
plt.legend()
plt.xlabel('-log(alpha)')
plt.ylabel('Mean squared error')
plt.title('Mean squared error on each fold')
         

# MSE from training and test data
from sklearn.metrics import mean_squared_error
train_error = mean_squared_error(tar_train, model.predict(pred_train))
test_error = mean_squared_error(tar_test, model.predict(pred_test))
print ('training data MSE')
print(train_error)
print ('test data MSE')
print(test_error)

# R-square from training and test data
rsquared_train=model.score(pred_train,tar_train)
rsquared_test=model.score(pred_test,tar_test)
print ('training data R-square')
print(rsquared_train)
print ('test data R-square')
print(rsquared_test)
 

Random Forests

Dataset
Same as Decision Trees assignment, I am using Gapminder dataset for the purpose of running Random Forest experiment

Data Management
Similar to previous assignment, I am using binary categorical response variable, ‘polityscore’ and a number of quantitative explanatory variables. The variable polity score ranges from -10 to 10. -10 to -5 is considered Autocratic. -5 to 5 is considered Anocratic. Countries falling in this range is usually politically neutral. 5 to 10 is Democratic. The variable is re-coded such that if a country is Autocratic or Democratic, then the value is 1. Otherwise the value is 0

The Random Forest
The code (last section of the post) is similar to decision tree experiment from previous assignment. The Random Forest Classifier is initialized with 25 estimators. That is, the random forest will be comprised of 25 trees

Shape of training and test samples

The figure above shows the shape of the training and test samples. 87 observations, 60% of the dataset is used as training set. The remaining 40% or 59 observations are used as test set. There are 3 predictors or response variables used in this example.

Correct and incorrect classification matrix

The figure above shows the output of confusion matrix. The diagonal, 5, 44 reflects the number of true negatives and true positives respectively. The diagonal 5, 5 reflects the false negatives and false positives for the variable polity score. Where value of 1 for the variable means the country is politically biased, i.e autocratic and democratic. 0 implies the country is neutral

The accuracy of the model came up as 0.830508474576. Approximately 83% of the sample of countries was classified correctly as having a political bias or not having a political bias.

Measured Importance of Explanatory Variables (Features)

Measured importance of explanatory variables or Features

From the above figures, variable with highest importance score: Internet Use Rate with score of 0.19749606 and variable with lowest importance score: Employment Rate with score of 0.10237368.

Correct classification rate for different number of trees

We saw above that accuracy of the classification was predicted as 83%. We have used 25 trees in our random forest experiment to achieve this. The figure below shows the accuracy score plotted against number of trees. The figure gives us an idea is 25 trees were indeed needed to achieve the accuracy score of 83

From the above plot we see that for 6, 14, 18 and 23 accuracy can be actually higher than our chosen number, which is 25.

Code

Random Forest Code

Decision Trees

Dataset

I am using the Gapminder dataset. Decision tree analysis was performed to test nonlinear relationships among a series of explanatory variables and a binary, categorical response variable.

Data Management

The Gapminder dataset does not have any binary categorical variable. So, I have converted the variable ‘polityscore’ into a binary categorical variable. The variable polity score ranges from -10 to 10. -10 to -5 is considered Autocratic. -5 to 5 is considered Anocratic. Countries falling in this range is usually politically neutral. 5 to 10 is Democratic. The variable is recoded such that if a country is Autocratic or Democratic, then the value is 1. Otherwise the value is 0.

The Decision Tree

Above decision tree is constructed with response variable or target as polity score and 3 quantitative explanatory variables or predictors - internet use rate, female employment rate and urban population rate. Looking at the tree from top to bottom (depth first), the first split (first node) is based on X[0] <= 38.05. If internet use rate (X[0], or first explanatory variable) is less than 38.05% move to left branch. Otherwise go right. In the second level the split is based on the second explanatory variable (X[1]), female employment rate. In this fashion the tree grows recursively splitting on certain condition imposed on the explanatory variables. One can follow the tree in a depth first fashion and reach one of the leaves which shows the values of response variable as a result of the decisions made along the branches.

 Shape of the training and test samples

The above output shows the shape of the training and test samples. 87 observations, 60% of the dataset is used as training set. The remaining 40% or 59 observations are used as test set. There are 3 predictors or response variables used in this example.

Correct and Incorrect classification of Decision Tree

The diagonal, 11, 35 reflects the number of true negatives and true positives respectively. The diagonal 5, 8 reflects the false negatives and false positives for the variable polity score. Where value of 1 for the variable means the country is politically biased, i.e autocratic and democratic. 0 implies the country is neutral.

The accuracy of the model came up as 0.779661016949

Code

# -*- coding: utf-8 -*-
"""
Created on Sat Feb  6 23:33:14 2016

@author: Abhishek
"""
from pandas import Series, DataFrame
import pandas
import numpy as np
import os
import matplotlib.pylab as plt
from sklearn.cross_validation import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import classification_report
import sklearn.metrics

#os.chdir("C:\Data Analysis and Interpretation")

"""
Data Engineering and Analysis
"""
#Load the dataset

data = pandas.read_csv('gapminder.csv')

# Replace empty values with NaN
data['polityscore'] = data['polityscore'].astype(np.object)
data['polityscore'] = data['polityscore'].replace(' ',np.nan)
data['polityscore'] = data['polityscore'].replace('',np.nan)

data['femaleemployrate'] = data['femaleemployrate'].astype(np.object)
data['femaleemployrate'] = data['femaleemployrate'].replace(' ',np.nan)
data['femaleemployrate'] = data['femaleemployrate'].replace('',np.nan)

data['internetuserate'] = data['internetuserate'].astype(np.object)
data['internetuserate'] = data['internetuserate'].replace(' ',np.nan)
data['internetuserate'] = data['internetuserate'].replace('',np.nan)

data['urbanrate'] = data['urbanrate'].astype(np.object)
data['urbanrate'] = data['urbanrate'].replace('',np.nan)
data['urbanrate'] = data['urbanrate'].replace(' ',np.nan)

# Target Variable
data['polityscore'] = pandas.to_numeric(data['polityscore'], errors='coerce')

# Predictor Variables
data['femaleemployrate'] = pandas.to_numeric(data['femaleemployrate'], errors='coerce')
data['internetuserate'] = pandas.to_numeric(data['internetuserate'], errors='coerce')
data['urbanrate'] = pandas.to_numeric(data['urbanrate'], errors='coerce')

data_clean = data.dropna()

#print(data_clean.dtypes)
#print(data_clean.describe())

#%%
# Data Management: Polity Score is chosen as the response variable. 
# -10 to -5: Autocratic, -5 to 5: Anocratic and 5 to 10: Democratic
# Here, Anocratic countries are coded as 0 and countries with political 
# biases are coded as 1. Hence we have out bivariate response variable

def RecodePolityScore (row):
   if row['polityscore']<=-5 or row['polityscore']>=5 :
      return 1
   elif row['polityscore']>-5 and row['polityscore']<5 :
      return 0
       

# Check that recoding is done      
data_clean['polityscore'] = data_clean.apply(lambda row: RecodePolityScore(row),axis=1)
chk1d = data_clean['polityscore'].value_counts(sort=False, dropna=True)
print (chk1d)

#%%
"""
Modeling and Prediction
"""
#Split into training and testing sets

predictors = data_clean[[
'internetuserate',
'femaleemployrate',
'urbanrate'
]]

targets = data_clean.polityscore

pred_train, pred_test, tar_train, tar_test  =   train_test_split(predictors, targets, test_size=.4)
print("Shape")
print("-----")
print(pred_train.shape)
print(pred_test.shape)
print(tar_train.shape)
print(tar_test.shape)

#Build model on training data
classifier=DecisionTreeClassifier()
classifier=classifier.fit(pred_train,tar_train)

predictions=classifier.predict(pred_test)

print("Predictions")
print("-----------")
print(sklearn.metrics.confusion_matrix(tar_test,predictions))
print("Accuracy of the Model")
print("---------------------")
print(sklearn.metrics.accuracy_score(tar_test, predictions))

#Displaying the decision tree
from sklearn import tree
#from StringIO import StringIO
from io import StringIO
#from StringIO import StringIO 
#from IPython.display import Image
out = StringIO()
tree.export_graphviz(classifier, out_file=out)
import pydot_ng as pydotplus
graph=pydotplus.graph_from_dot_data(out.getvalue())
with open('DecisionTree.png', 'wb') as f:
    f.write(graph.create_png())